By Noel Huntley, Ph.D.

An atom, or any such basic entity, cannot have symmetry, for example, be spherical, and be stable, unless its formative energies utilise the fourth dimension. In fact its geometry extends along the gradient 3rd to 4th dimension and takes the shape of a toroid, or doughnut from a 4D view. More correctly this is a 4D-to-3D vortex.

At the time of the renowned physicist Lord Kelvin, the vortex theory was popular, along with the recognition of the ether medium through which electromagnetic waves could travel. Modern physics, the Michelson-Morley experiment, and in particular Einstein and relativity put an end to these essential ideas—vortex and the ether.

The ether was abandoned since it couldn’t be detected; moreover because a covariant ether theory—necessary for good physics and the test-of-truth requirements—wasn’t understood. Vortex theories were numerous, more so even recently by new-science pioneers (frowned on by academics). However, all such vortex theories, which have included toroid-shaped vortex rings (2D-3D) and spherical (3D) vortices, fail to interest anyone but the few and in particular fail all the tests of truth of modern physics, such as supersymmetry, nonpreferential axes (at least in 3D), and generalisation.

Fortunately, and quite magically, if one adds another dimension, the perfect geometry comes into view. Imagine the toroid, or an actual doughnut. It has a preferential axis about which it has symmetry, that is, it does not look the same from every angle (only a sphere does). Nevertheless, it is a good 3D-to-2D dimensional model for our purposes.

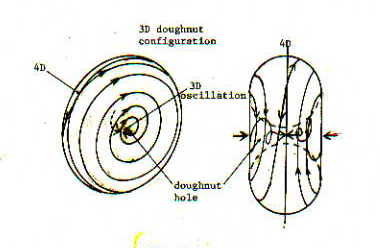The energy form we must visualise is 4D to 3D , that is, one extra dimension must be added to the common doughnut shape. This results in a symmetrical entity in 3D, that is, a sphere. Now let us switch back to the 3D-to-2D doughnut. If we draw a plane through this toroid so that there is symmetry on each side of the plane, that is, one side is the mirror image of the other, these two sides represent a dual-polarity system. On the 4D-to-3D model this means the whole sphere is only one pole. Where is the other?

If one moves one’s consciousness through the surface of an atom and follows a radius to the centre, what will happen? Initially, picture the 3D-to-2D doughnut, one that is thick with a small hole in the centre. If one moves into this hole from one side by sliding down the surface, and instead of going across the hole to the opposite part on the same side, one goes through the hole and out of the other side, it will appear as though one has flipped over and is returning on the same side. Not only is it the other, mirror-image side but if one follows the surface it will return to the same starting point on the outer edge, representing the unity of both poles!

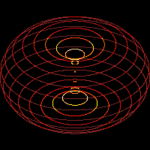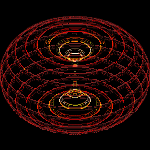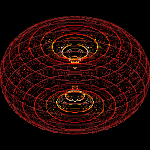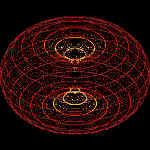Similarly with the 4D-to-3D toroid. By following the radius down one spherical pole instead of going across the centre of the same sphere, curve through the hole into the 4th dimension and it will appear as though one is returning along the same path. However, one is now in an identical anti-universe space, the opposite side or pole, in this 4D-to-3D oscillation. By continuing along this path one eventually returns to the starting point (which is actually beyond the surface of the atom—greater radius—and displaced 4th dimensionally.

One may see why such basic particles as an electron must be ‘turned’ twice 360 degrees to return to their original orientation—not 360 degrees as with a 3D sphere such as a ball. This is also the reason for Dirac’s discovery of negative electrons and antiparticles. The ‘coin’ has two sides, matter/antimatter—half an oscillation each—and cannot exist without these two sides. We in 3D only perceive one side of the ‘coin’. The basic energy unit also explains the strange mirror-image properties found in particle physics studies.

What is this starting point, that is, the 4D unity of the two poles? It is the surface of a 4D vortex, which as we have seen has not one—as in a 3D sphere—but two spirals towards its centre (use the 3D-to-2D doughnut model) where they meet, creating a standing wave/stationary state/oscillation, which manifests in our 3D space like an alternate explosion and implosion. This means that we ‘see’ only the centre portion of, say, an atom’s full vortex.

If one wishes to use the tesseract model it has limited but useful application . Instead of cubes within cubes visualise spheres within spheres—close in size (touching). Pick one sphere as representing the 3D object. (This will have a particular range of frequencies corresponding to the 3rd dimension.) Now as one envisages the circles reaching the smallest size one must imagine they continue through the point and gradually become larger on the other side. Any two corresponding circles, one on each side, can form a fractal level or entity. Each pair represents a dual polarity and an inherent oscillation—a double helix spiral.

As an example, a planet vortex will spiral in to all its atoms or other sub-entities (this is hierarchical). The planet oscillation, however, will contain in its own format all sub-frequencies, such as of atoms. A cell, for example, is a whole unit oscillation of complex programmed modulations, and is the master control over its constituents but in turn it is an element in a greater whole—an organ, etc.

If one begins with the universe vortex, one should picture it spiralling in then branching off into slightly smaller vortices representing, say, supercluster galaxy entities. Each of the latter are then visualised as spiralling in to further offshoots, which would be galaxy clusters, and from these, galaxies branching off to groups of solar systems, individual solar systems then planets, atoms, etc. Thus every particle is connected to the universe oscillation through the fractal levels of planets, star systems, galaxies, etc. But remember that each of these spirals meets its opposite to create the stable oscillation or stationary state.

Now the frequency increases from particles, through the gradient, to universe. For a possible explanation: the greater the wholeness, quantum state, or integration, the greater the frequency—if the interaction or interface of the two spirals is greater one could consider the force between them would be greater and therefore the frequency. In addition, the larger the entity the more elements and fractal levels it contains, and therefore must be more intelligent, of which a higher rate of creation (frequency) is a requirement.

These central oscillations within different vortices can be out of phase with one another giving us a proper definition of 3D spacetime—homogeneous distribution of particles/oscillations out of phase with one another. However, at the surface of the 4D vortices we have harmony. The vortices are in phase—different realities exist at this level.

It is relevant to note that the brilliant philosopher professor Charles Hinton worked out that 4D rotations of such 4D spheres can all be in phase, be self-supporting, forming what he called a ‘self-preservative living system’. Whereas if we try rotating 3D spheres in a group which are touching, some of their motions will be contrary.

It is vital that one eradicates the simple Newtonian picture of objects in empty space, of a background absolute time and a flat continuous one-level spacetime. Between the 4D surface of the vortex and its 3D center there are countless spacetime frames each in the context of the next higher one. There is a gradient of increasing correlation of frequencies from the 3D out-of-phase condition to the 4D periphery of the vortex, where cyclic action of the positive and negative occur; the positive and negative ‘following’ one another cyclically around the ‘surface’. Note that quantum reduction occurs down the gradient from 4D to 3D between any levels, whereas in current quantum theory, quantum reduction occurs between two levels: the quantum reality of phase-correlation (many probabilities) to the material reality of phase-randomisation (one probability). Also quantum regeneration occurs up the gradient from lesser wholes to greater wholes (by correlating lesser wholes)—not recognised in current science.

Worlds, universes, can be structured at any of these levels of spacetime. Change of frequency-range keeps them segregated. Thus these worlds will have matter structured from fully opposing flows at the 3D level through a gradient of less opposition and greater integration between the positive and negative to the harmonious cyclic flows, in which the positive and negative poles aid one another in forming the cyclic energies around the vortex periphery.

The reader may still be asking: Why vortices? Why does energy spiral? We have answered this briefly. It is a matter of 4D geometry, 4D oscillations, and transduction of energies from a 4D format to a 3D format. The energy must spiral to achieve this and in turn it creates a perfect contextual system—like spheres within spheres—all ‘touching’. It does not take place in any space; it creates space itself at different dimensional levels.

Note that this fundamental higher-dimensional energy configuration is a scalar phenomenon. It consists of two opposite centripetal spirals and is the basis of the so-called (within the New-Age field) Merkaba. Everything that is created will have a Merkaba field, enabling energies to transduce across dimensions.

More on the vortex theory: